20 января 2015г. в школе № 5 г.Коряжмы прошла игра «Математические бои» в рамках недели «МИФ», в которой приняли участие 2 команды из учеников 8-9 классов.
Цель мероприятия:
- пропаганда математики среди учащихся;
- подготовка учащихся к городской игре «Математические бои».
Организатор мероприятия: Ярославцева Е.В.
Члены жюри: Патрина В.А., Петрова О.Г., Бурова Е.П.
Состав команд: «Часы» (капитан Власенков Павел) и «Куб» (капитан Соболева Анастасия):
|
1 команда: 1) Ведерников Даниил -9а класс 2) Бызов Вадим – 9а класс 3) Власенков Павел – 9а класс 4) Бегоулев Антон – 8а класс 5) Лысцев Кирилл – 8а класс 6) Ядрихинский Кирилл – 8а класс |
2 команда: 1) Синицкий Даниил -9б класс 2) Соболева Анастасия – 9б класс 3) Старова Дария – 9б класс 4) Нюхина Нелли – 8б класс 5) Гарджук Анна – 8б класс 6) Бебякина Евгения – 8б класс |
Задания и ответы для «Математических боёв» 20.01.2015 (школьный уровень)
1. На столе лежит 36 шариков. Кощей и Василиса Премудрая играют в игру. Каждый из них по очереди разбивает шарики на группы (может быть на одну), в каждой из которых равное число шариков. Число групп не может повторяться. Проигрывает тот, кто не сможет найти новое разбиение. Кто выиграет игру, если начал игру Кощей?
Решение: задача сводится к нахождению числа различных делителей числа 36. Возможны делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36, то есть всего 9. Получили нечётное число делителей, значит закончит игру тот, кто её начал.
Ответ: выиграет Кощей
2. На плоскости даны 2010 точек, никакие три из которых не лежат на одной прямой. Доказать, что найдётся треугольник с вершинами в этих точках, не содержащий ни одной из оставшихся точек.
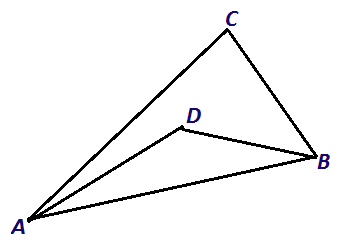Решение: воспользуемся принципом крайнего. Рассмотрим треугольник ABC наименьшей площади. Тогда он не может содержать других точек: если внутри него лежит точка D (смотри рисунок), то площадь треугольника ADB меньше, что противоречит выбору треугольника. Значит, треугольник АВС не содержит ни одной из оставшихся точек. Ч.т.д.
3. Крестьянин пришёл к царю и попросил: «Царь, позволь мне взять 1 яблоко из твоего сада». Царь ему разрешил. Пришёл крестьянин к саду и видит: весь сад огорожен тройным забором. Каждый забор имеет только одни ворота, и около каждых ворот стоит страж. Подошёл крестьянин к первому стражу и сказал: «Царь разрешил мне взять 1 яблоко из сада». «Возьми, но при выходе должен будешь отдать мне половину яблок, что возьмёшь, и ещё одно», - поставил условие страж. Это же повторили ему второй и третий стражи. Сколько яблок должен взять крестьянин в саду, чтобы стражи получили свою долю, а у него осталось 1 яблоко?
Решение: решим задачу с конца. Перед последними воротами у крестьянина должно остаться (1+1)×2=4 яблока, перед вторыми – (4+1)×2=10 яблока и перед первыми - (10+1)×2=22 яблока.
Ответ: 22 яблока.
4. Как с помощью циркуля и линейки разделить угол величиной 19° на 19 равных частей? Найдите несколько способов решения.
Решение:
1 способ. Построим окружность с центром в вершине угла, отложим на ней 19 раз угол 19°. В результате получим угол в 1°= 19° ×19 - 360°. С помощью этого угла делим данный угол на 19 частей.
2 способ. Отложим 5 раз угол 19°, в итоге получим угол 95° . Построим прямой угол и найдем разность 95° и 90° , равную 5° , тогда 1° = 5° × 4 - 19° . Далее поступаем так же, как и в первом случае.
Результаты: обе команды выступали достойно, показывая хорошие умения и навыки решения олимпиадных задач. Но из-за стратегической ошибки ведения боя командой «Куб», победу, со счетом 13 : 12, одержала команда «Часы».