«Математическая драка»

28 января 2015г. в нашей школе впервые прошла игра «Математическая драка» в рамках недели  «МИФ», в которой приняли участие 3 команды из учеников 7-х классов.

Основными видами математических соревнований являются олимпиады (стандартные и нестандартные, личные и командные), бои, карусели, викторины, конкурсы и т.д.

Математическая драка является разновидностью личной (командной) олимпиады и относится к нестандартным олимпиадам. Учащимся необходимо проявлять не только умения решать олимпиадные задачи, но и продумывать стратегии ведения боя, умело распоряжаться математической валютой (тугрики), дающей право заявляться на бой.

Цель мероприятия:

• пропаганда математики среди учащихся;
• обучение  учащихся решать олимпиадные задач.

Организатор мероприятия: Ярославцева Е.В., Петрова О.Г.

Члены жюри: Патрина В.А.,  Петрова О.Г., Ярославцева Е.В.

Состав команд:

Задания с ответами для «Математической драки»

1. У овец и кур вместе 36 голов и 100 ног. Сколько овец? (2 тугрика)

Решение:

1) 36*2 = 72 (ног) – если бы все животные ходили на 2-х ногах;

2) 100 - 72 = 28 (ног) – «лишние» ноги, принадлежащие четырёхногим животным

3) 28 : 2 = 14 (овец)

Ответ: 14 овец

2. Перед вами стоят 6 стаканов: три с водой и три пустых (смотри рисунок). Дотроньтесь рукой лишь до одного стакана и добейтесь, чтобы пустые и полные стаканы чередовались. (2 тугрика)

Решение: перелить воду из второго стакана в пятый.

3. Решите ребус, если одинаковые цифры обозначены одинаковыми буквами, а разные цифры – разными (4 тугрика):

ВАГОН + ВАГОН = СОСТАВ 

Решение: 85 679 + 85 679 = 171 358

4. Алёша, Боря и Витя учатся в одном классе. Один ездит домой из школы на автобусе, другой – на трамвае, третий – на троллейбусе. Однажды после уроков Алёша пошёл проводить друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из автобуса: «Боря, ты забыл в школе тетрадь!» Кто на чём ездит домой? (2 тугрика)

Решение: так как Алёша не ездит на троллейбусе и провожает друга до автобусной остановки, то он ездит на трамвае. Так как третий друг кричал Боре из троллейбуса, то Боря ездит на автобусе, а третий друг – Витя – на троллейбусе.

Ответ: Алёша – трамвай; Боря – автобус; Витя – троллейбус.

5. Игнату сейчас вчетверо больше лет, чем было его сестре в тот момент, когда она была вдвое моложе его. Сколько лет сейчас Игнату, если через 15 лет ему и сестре будет вместе 100 лет? (4 тугрика)

Решение: по условию задачи составим таблицу:

Уравнение: (4x+15)+(3x+15)=100, откуда x=10, тогда Игнату сейчас 40 лет

Ответ: 40 лет

6. В вершинах куба записаны числа 2, 0, 0, 3, 1, 9, 5, 7. За один ход разрешается прибавить к числам, стоящим на концах одного ребра, одно и то же целое число. Можно ли за несколько ходов получить нули во всех вершинах? (6 тугриков)

Решение: 2+0+0+3+1+9+5+7=27 – сумма всех чисел в вершинах куба первоначально; 27 – нечётное число. При прибавлении двух одинаковых чисел четность не изменится: ч+ч+н= или н+н+н=н. А так как 0+0+0+0+0+0=0 – чётное число, то получить нули во всех вершинах куба нельзя.

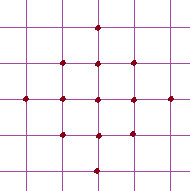
7. На рисунке изображены 13 точек. Сколько квадратов с вершинами в этих точках можно нарисовать? (Все точки располагаются в вершинах квадратиков со стороной 1) (4 тугриков)

Решение: 11 квадратов.

8. 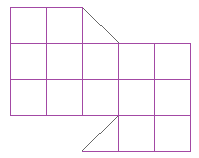Разрежьте фигуру на 2 равные части. (4 тугрика)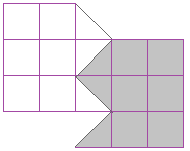

9. Аня и Таня вместе весят 40кг, Таня и Маня – 50кг, Маня и Ваня – 90кг, Ваня и Даня – 100кг, Даня и Аня – 60кг. Сколько весит Аня? (6 тугриков)

Решение:

1) 40+50+90+100+60=340(кг) – удвоенная масса всех ребят

2) 340:2=170(кг) – масса всех ребят

3) 50+100=150(кг) – масса Тани, Мани, Вани, Дани

4) 170-150=20(кг)- весит Аня

Ответ: 20 кг

10. Из бочки, содержащей не менее 10л бензина, отлейте ровно 6л, используя бидон вместительностью 5л и девятилитровое ведро. (4 тугрика)

Решение: 

Результаты игры

Результаты представлены таблицей:

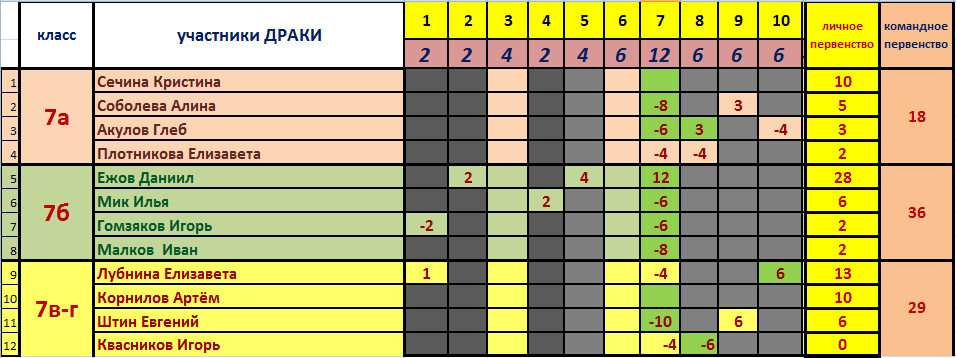
С учётом правил игры, лидерами стали:

Личное первенство: 1 место – Ежов Даниил (7б класс), 2 место – Лубнина Елизавета (7в класс), 3 место – Штин Евгений (7г класс);

Командное первенство: 1 место – 7б класс, 2 место – 7в и 7г классы, 3 место – 7а класс.